Question

Find the explicit formula.-30, -26, -22, -18,….34, -166, -366, -566,…

Answer 1

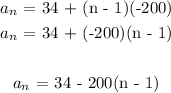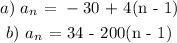
`\begin{gathered} a)\text{ }a_n\text{ = }-30\text{ + 4(n - 1)} \\ b)\text{ }a_n\text{ = 34 - 200(n - 1)} \end{gathered}`Step-by-step explanation:

a) -30, -26, -22, -18,….

We need to find out if the sequence is arithmetic or geometric.

the common difference = next term - previous term

the common difference = -26 - (-30) = -26 + 30

the common difference = 4

the common difference = -22 - (-26) = -22 + 26

the common difference = 4

Hence, the common difference is constant. This makes it arithmetic

`\begin{gathered} \text{The formula for arithmetic sequence:} \\ a_n=a_1\text{ + (n-1)d} \\ \text{where }a_1\text{= first term, d = common difference} \\ n\text{ = number of terms} \\ a_n\text{ = nth term} \end{gathered}`

First term = -30, d = 4

The explicit formula becomes:

`\begin{gathered} a_n\text{ = }-30\text{ + (n - 1)}4 \\ a_n\text{ = }-30\text{ + 4(n - 1)} \end{gathered}`

b) 34, -166, -366, -566,…

let's find the common difference:

common difference = next term - previous term

common difference = -166 - 34 = -200

common difference = -366 - (-166) = -366 + 166 = -200

The common difference is constant. This is arithmetic

`\begin{gathered} \text{The formula for arithmetic sequence:} \\ a_n=a_1\text{ + (n-1)d} \\ a_1\text{ = first term = 34,} \\ \text{ d = common difference = -200} \end{gathered}`

The explicit formula becomes:

`\begin{gathered} a_n\text{ = 34 + (n - 1)(-200)} \\ a_n\text{ = 34 + (-200)(n - 1)} \\ \\ a_n\text{ = 34 - 200(n - 1)} \end{gathered}`