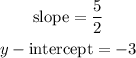Question

Identify slope and y-intercept of the equation. 5x -2y=6

Answer 1

As given by the question

There are given that the equation:

`5x-2y=6`

Now,

To find the slope and y-intercept, first we need to rewrite the given equation into the standard form, y = mx + b

Where, m is slope and b is y-intercept.

Then,

From the given equation:

`5x-2y=6`

Subtract 5x from both sides of the equation

So,

`\begin{gathered} 5x-2y=6 \\ 5x-2y-5x=6-5x \\ -2y=6-5x \end{gathered}`

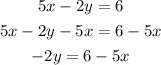
Then,

Divide by -2 on both sides of the equation:

So,

`\begin{gathered} -2y=6-5x \\ (-2y)/(-2)=(6)/(-2)-(5x)/(-2) \\ y=-3+(5)/(2)x \\ y=(5)/(2)x-3 \end{gathered}`

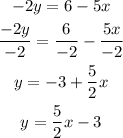
Then,

After compare with standard equation, y = mx + b

The value of slope and the y-intercept is shown below:

`\begin{gathered} \text{slope}=(5)/(2) \\ y-\text{intercept}=-3 \end{gathered}`