The equation of the line with slope m and y-intercept b is given by:

In this case the slope is 5 and the y-intercept is -2; then we have that the equation of the line is:
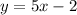
Now that we have the equation of the line we can use it to find points on the line, we do that by given values to x (whichever values we want) and use the equation to determine its corresponding y value.
If x=0, then we have:
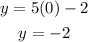
Hence, the line passes through the point (0,-2).
If x=1, then we have:
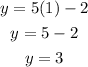
Hence, the line passes through the point (1,3).
Now that we have two points on the line we graph them on the plane:
Finally, we join the points with a straight line. Therefore, the graph of the line is: