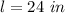Question

The width of a rectangular picture is one-half the length. The perimeter of the rectangle is 72 inches. Find the length of the picture.

Answer 1

Given that the width of the rectangular piccture is:

`w=(1)/(2)l`

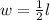
Where "l" is the length of the picture.

You know that the perimeter is:

`P=72\text{ }in`

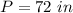
The formula for calculating the perimeter of a rectangle is:

`P=2l+2w`

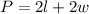
Where "l" is the length and "w" is the width.

Therefore, you can substitute the perimeter and the width into the formula, in order to find "l":

`72=2l+2((1)/(2)l)`

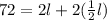
Now you can solve for "l":

`72=2l+(2)/(2)l`
`72=2l+l`
`72=3l`
`(72)/(3)=l`
`l=24\text{ }in`

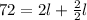
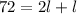
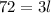
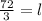
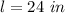
Hence, the answer is:

`l=24\text{ }in`