Given:
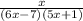
Required:
We need to find the partial decomposition of the given rational expression.
Step-by-step explanation:
Use the partial decomposition formula.
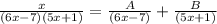
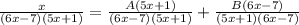
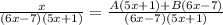
Equate the numerator of both sides since the denominator of both sides of the equation is equal.
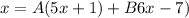
Set x =-1/5 and substitute in the equation to find the value of B.

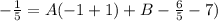
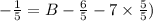
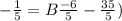

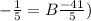
Solve for B.
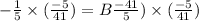
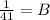
We get B=1/41.
Set x =0 and substitute x=0 and b =1/41 in the equation to find the value A.
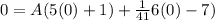
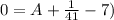
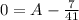
Solve for A.

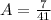
We get A=7/41.

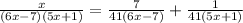
Final answer:
