Question

What is the angular speed and the speed of the cyclist?

Answer 1

Given data:

* The frequency of the revolution is f = 290 rev/min.

* The diameter of the wheels is d = 1.8 feet.

Solution:

The angular speed of the wheel is,

`\begin{gathered} \omega=2\pi f \\ \omega=2\pi*290 \\ \omega=1822\text{ radians/min} \end{gathered}`

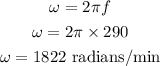
Thus, the angular speed of the wheel is 1822 radians/minute.

(b). The radius of the wheels is,

`\begin{gathered} r=(d)/(2) \\ r=(1.8)/(2) \\ r=0.9\text{ ft} \end{gathered}`

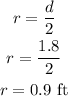
The linear speed of cyclist is,

`\begin{gathered} v=r\omega \\ v=0.9*1822 \\ v=1640\text{ ft/min} \end{gathered}`

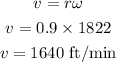
Thus, the linear speed of the cyclist is 1640 feet/minute.