We have the system of equations:
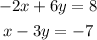
We can solve it by substituttion: we can clear the value of x in terms of y from the second equation and replace it in the first one.

Then, if we replace x in the first equation, we can solve for y:
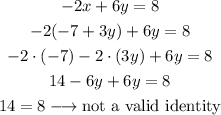
From the final result, we can conclude that there is no value of x and y that is a solution to the system, as we end with an invalid identity, as 14 is not equal to 8.
In a graphical form, the equations of the system are parallel lines that do not intersect in any finite point (x,y).
We can see that they are parallel when we divide the first equation by -2 and compare:
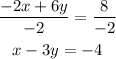
if we compare it with the second equation:
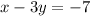
we can see that the slope is the same, but the intersect are different.
In a graph, the equations look like:
They are parallel and do not intersect in any finite point (x,y).
Then, in conclusion, the system has no solution.