Question

Hello help me with this question thanks in advance​

Answer 1

`\bold{\huge{\green{\underline{ Solutions }}}}`

Answer 11 :-

We have,

`\sf{HM = 5 cm }`

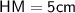
• In square all sides of squares are equal

The perimeter of square

`\sf{ = 4 × side }`

`\sf{ = 4 × 5 }`

`\sf{ = 20 cm }`

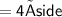
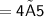
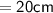
Thus, The perimeter of square is 20 cm

Hence, Option C is correct .

Answer 12 :-

We have,

`\sf{MX = 3.5 cm }`

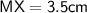
• In square, diagonals are equal and bisect each other at 90°

Here,

`\sf{MX = MT/2}`

`\sf{MT = 2 * 3.5 }`

`\sf{MT = 7 cm}`

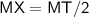
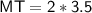
Thus, The MT is 7cm long

Hence, Option C is correct .

Answer 13 :-

We have to find the measure of Angle MAT

• All angles of square are 90° each

From above

`\sf{\angle{MAT = 90° }}`

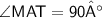
Thus, Angle MAT is 90°

Hence, Option B is correct .

Answer 14 :-

We know that,

• All the angles of square are equal and 90° each

Therefore,

`\sf{\angle{MHA = }}{\sf{\angle{ MHT/2}}}`

`\sf{\angle{MHA = 90°/2}}`

`\sf{\angle {MHA = 45°}}`

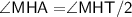
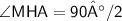
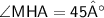
Thus, Angle MHA is 45°

Hence, Option A is correct

Answer 15 :-

Refer the above attachment for solution

Hence, Option A is correct

Answer 16 :-

Both a and b

• The median of isosceles trapezoid is parallel to the base
• The diagonals are congruent

Hence, Option C is correct

Answer 17 :-

In rhombus PALM,

• All sides and opposite angles are equal

Let O be the midpoint of Rhombus PALM

In ΔOLM, By using Angle sum property :-

`\sf{35° + 90° + }{\sf{\angle{ OLM = 180°}}}`

`\sf{\angle{OLM = 180° - 125°}}`

`\sf{\angle{ OLM = 55° }}`

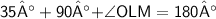
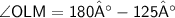
Now,

`\sf{\angle{OLM = }}{\sf{\angle{OLA}}}`

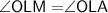
• OL is the bisector of diagonal AM

Therefore,

`\sf{\angle{ PLA = 55° }}`

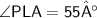
Thus, Angle PLA is 55° .

Hence, Option C is correct