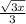Given:
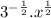
To find:
Express with radical signs instead of fractional exponents. also, rationalize the denominator.
Step-by-step explanation:
The radical sign is a symbol used to indicate a root, i.e.,
![\sqrt[n]{x}](https://img.qammunity.org/2023/formulas/mathematics/high-school/82umi5h7pf7ttup974ahitbbdz5w1ee0u3.png)
For our given expression, we can write it using the radical sign as given below:
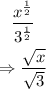
Now, to rationalize, the following form can be used,
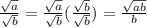
So, we can also rewrite our expression to rationalize the denominator,
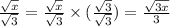
Final answer:
The required expression with radical signs and simplified form is as given below: