We will investigate the number of calories in ice cream and pie. We will define the variables as such:
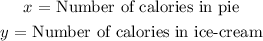
From the given data a relationhsip between the number of calories in a pie ( x ) and the number of calories in an ice-cream scoop are given by the following statement:
" The number of calories in a piece of pie is 20 less than three times the number of calories in a scoop of ice cream. "
We will go ahead and decrypt the above given statement and express it mathematically in terms of declared variables ( x and y ) as follows:

The next statement gives us the combined calories in both ice-cream scoop and a pie:
" The pie and ice cream together have 500 calories. "
We will go ahead and decrypt the above given statement and express it mathematically in terms of declared variables ( x and y ) as follows:

We have two equations ( derived ) and two variables ( x and y ):
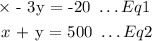
We will solve the two equations ( Eq1 and Eq2 ) simultaneously using elimation method as follows:
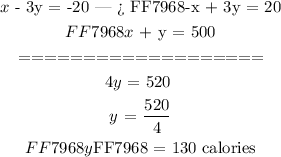
We first multiplied the ( Eq1 ) by ( -1 ) then added the modified ( Eq1 ) to ( Eq2 ) whilst eliminating ( x ) and solved for the number of calories in an ice-cream scoop ( y ) i.e 130 calories.
Then we will back substitute the value of ( y ) into ( Eq2 ) and solve for ( x ):
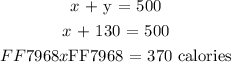
Therefore, the number of calories in each confectionary is as such:
