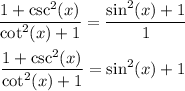Question

I need help in math can you please help me 0

Answer 1

We will use the following identities:

`\begin{gathered} \csc (x)=(1)/(\sin (x)) \\ \cot (x)=(\cos (x))/(\sin (x)) \end{gathered}`

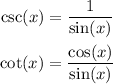
So, replacing the identities on the left side, we get:

`(1+\csc^2(x))/(\cot^2(x)+1)=(1+((1)/(\sin(x)))^2)/(((\cos (x))/(\sin (x)))^2+1)`

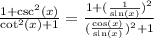
Then, solving the power and adding the expressions, we get:

`(1+csc^2(x))/(\cot^2(x)+1)=(1+(1)/(\sin^2(x)))/((\cos^2(x))/(\sin^2(x))+1)`
`(1+csc^2(x))/(\cot^2(x)+1)=((\sin^2(x)+1)/(\sin^2(x)))/((\cos ^2(x)+\sin ^2(x))/(\sin ^2(x)))`

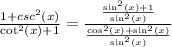
Dividing the expression and simplifying, we get:

`(1+csc^2(x))/(\cot^2(x)+1)=(\sin ^2(x)+1)/(\cos ^2(x)+\sin ^2(x))`

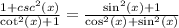
Finally, we know that cos²(x) + sin²(x) = 1, so we can rewrite the expression as:

`\begin{gathered} (1+\csc^2(x))/(\cot^2(x)+1)=(\sin ^2(x)+1)/(1) \\ (1+\csc^2(x))/(\cot^2(x)+1)=\sin ^2(x)+1 \end{gathered}`