Question

Convert the point to polar coordinates using the interval [0, 2\small \pi) for θ. Show all work.

Answer 1

We know that polar coordinates are defined as:

`\begin{gathered} r=\sqrt[]{x^2+y^2} \\ \theta=\tan ^(-1)((y)/(x)) \end{gathered}`

in this case we have the point (-2,-2); this means that x=-2 and y=-2. Plugging this value for the radius we have that:

`\begin{gathered} r=\sqrt[]{(-2)^2+(-2)^2} \\ r=\sqrt[]{4+4} \\ r=\sqrt[]{2\cdot4} \\ r=2\sqrt[]{2} \end{gathered}`

Plugging the values for the angle we have:

`\begin{gathered} \theta=\tan ^(-1)((-2)/(-2)) \\ \theta=\tan ^(-1)(1) \\ \theta=(\pi)/(4) \end{gathered}`

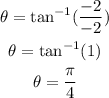
for the angle we need to be careful, we know that the point (-2,-2) in on the third quadrant, this means that the angle is greater than pi but when we use the formula we got pi/4; this comes from the fact that the formula for the angle determines the angle measure in the quadrant we are at. This means that we need to add the appropiate amount to the angle found by this formula to find the correct one. In this case, since we are on the third quadrant, we need to add pi to the angle we found, then we have:

`\begin{gathered} \theta=(\pi)/(4)+\pi \\ \theta=(\pi+4\pi)/(4) \\ \theta=(5\pi)/(4) \end{gathered}`

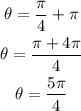
Hence the correct angle is 5pi/4.

Therefore the polar coordinates of the angle are:

`(2\sqrt[]{2},(5\pi)/(4))`