Given that you drop a rock into a well, then you hear the splash 1.5 seconds later.
Let's solve for the following:
(a) How deep is the well?
To find the depth of the well, apply the formula:
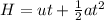
Where H is the depth of the well
t is the time = 1.5 seconds
a is acceleration due to gravity = 9.8 m/s²
u is the initial velocity = 0 m/s
Thus, we have:
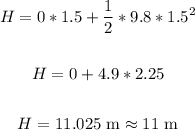
The depth of the well is 11 meters.
(b). If the depth of the well were doubled, would the time required to hear the splash be greater than, less than, or equal to 3.0 seconds?
If the depth were doubled,