Question

Use the discriminant, b^2 - 4ac, to determine the number of solutions of the following quadratic equation. 7y^2 + 2 = -4yThen solve the quadratic equation using the formula y = (formula is in the pic attached)

Answer 1

2 non-real solutions and are as follows:

`\begin{gathered} x_1=-(2)/(7)+\frac{\sqrt[]{10}}{7}i \\ x_2=-(2)/(7)-\frac{\sqrt[]{10}}{7}i \end{gathered}`

Explanation:

The first thing we must do is convert the equation to the following form

`\begin{gathered} Ax^2+Bx+C=0 \\ \text{ We have the following equation:} \\ 7y^2+2=-4y \\ \text{now, we convert} \\ 7y^2+4y+2=0 \\ \text{therefore:} \\ a=7 \\ b=4 \\ c=2 \end{gathered}`

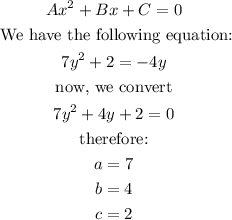
Now we calculate the discriminant

`\begin{gathered} d=b^2-4ac \\ \text{replacing} \\ d=4^2-4\cdot7\cdot2 \\ d=-40 \end{gathered}`

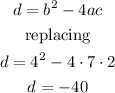
When the value of the discriminant is less than 0, the number of solutions is 2 and both are imaginary.

Now we calculate the solutions by means of the general equation, like this:

`\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ \text{replacing} \\ x_1=\frac{-4+\sqrt[]{4^2-4\cdot7\cdot2}}{2\cdot7}=-(2)/(7)+\frac{\sqrt[]{10}}{7}i \\ x_2=\frac{-4-\sqrt[]{4^2-4\cdot7\cdot2}}{2\cdot7}=-(2)/(7)-\frac{\sqrt[]{10}}{7}i \end{gathered}`