Question

A store has a sale with 12% off every item. When you enter the store, you receive a coupon that states you receive an additional 8% off the sale price. If you purchase an item that sells for $350, what will your total discount be (a) in dollar amount and (b) in percent?

Answer 1

a) To apply the first discount we need to calculate 12% of the price ($350).

`\text{ First discount = }350\text{ \$ }\cdot12\text{ \% = }350\cdot0.12=42\text{ \$}`

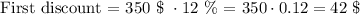
Considering this discount only, the cost of the product now is $350 - $42 = $308

Now, we need to apply the second discount to this new price. 8% of $308 is computed as follows:

`\text{ Second discount = }308\text{ \$ }\cdot8\text{ \% = }308\cdot0.08=24.64\text{ \$}`

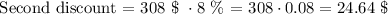
Then, the total discount is:

`\begin{gathered} \text{Total discount = first discount + second discount} \\ \text{Total discount = \$42 + \$24.64 } \\ \text{Total discount = \$}66.64 \end{gathered}`

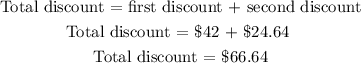
b) To calculate the total discount as a percent, we need to find what percent (x) represents $66.64 with respect to $350 (which represents 100%). We can do this with the help of the next proportion:

`\frac{350\text{ \$}}{66.64\text{ \$}}=\frac{100\text{ \%}}{x\text{ \%}}`

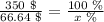
Solving for x:

`\begin{gathered} 350\cdot x=100\cdot66.64 \\ x=6664/350 \\ x=19.04 \end{gathered}`

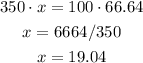
As a percent, the total discount is 19.04%