Question

Write an equation for a graph that is set of all points in the plane that are equidistant from the point f(-6,0) and the line x=6

Answer 1

x = - y^2/24

Step-by-step explanation:

Let (x,y) be an arbitrary point on the graph whose equation we seek, Then the distance of this point (-6, 0) is

`√((x-(-6))^2+(y-0)^2)`
`\Rightarrow√((x+6)^2+y^2)`

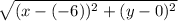
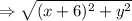
The distance from the line x = 6 is

`|x-6|`

Since the point (x,y) is equidistant from both the line and the point, the two expressions above must be equal:

`√((x+6)^2+y^2)=|x-6|`

Now we just have to convert the above into a form we can recognize.

Squaring both sides gives

`(x+6)^2+y^2=(x-6)^2`

subtracting (x+6)^2 from both sides gives

`y^2=(x-6)^2-(x+6)^2`

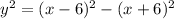
Expanding the right-hand side gives

`y^2=x^2-12x+36-x^2-12x-36`
`\Rightarrow y^2=-24x`

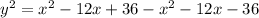
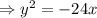
Solving for x gives

`\boxed{x=-(1)/(24)y^2.}`

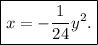
which is our answer!