Question

Solve for both variables. answer must be in simplest radical form.

Answer 1

Since we are dealing with a right triangle, we can use the following two trigonometric identities

`\sin \theta=(O)/(H),\cos \theta=(A)/(H)`

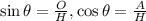
Where theta is an inner angle of the right triangle, A and O are the adjacent and opposite sides to theta, and H is the hypotenuse.

In our case,

`\sin (30dgr)=\frac{x}{22\sqrt[]{3}},\cos (30dgr)=\frac{y}{22\sqrt[]{3}}`

Thus,

`\begin{gathered} \Rightarrow x=22\sqrt[]{3}\sin (30dgr),y=22\sqrt[]{3}\cos (30\text{dgr)} \\ \Rightarrow x=\frac{22\sqrt[]{3}}{2}=11\sqrt[]{3},y=22\sqrt[]{3}(\frac{\sqrt[]{3}}{2})=11\cdot3=33 \\ \Rightarrow x=11\sqrt[]{3},y=33 \end{gathered}`

Hence, the answers are x=11sqrt(3) and y=33