To determine the length of the missing side AC, you have to apply the sine rule.
This rule states that the ratios between the sine of each angle and the side opposite to it are equal. For the given triangle the ratios can be determined as follows:
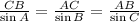
We know the measures of angles A and B and the side length AB. To determine the side length AC, the first step would be to calculate the measure of ∠C.
Considering that the sum of the inner angles of a triangle is 180º, you can calculate ∠C as follows:
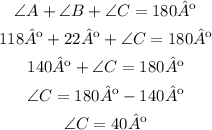
Now that we know that ∠C=40º, ∠B=22º, and AB=24, using the ratios described above you can determine side length AC as follows:
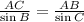
Multiply both sides by the sine of B to write the expression for AC
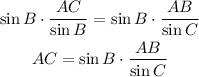
Replace the expression with the known values and calculate AC
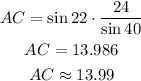
The length of AC is 13.99