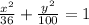Question

Write an equation for a vertical ellipse with major axis length 20, minor axis length 12 and its center at (0, 0).

Answer 1

The general formula for a vertical ellipse is:

`((x-h)^2)/(b^2)+((y-k)^2)/(a^2)=1`

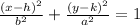
Where

(h,k) are the coordinates of the center.

a is the distance between the center and the vertices

b is the distance between the center and the co-vertices

For a vertical ellipse, the vertical axis is the major axis, and the horizontal axis is the minor axis, then a > b.

If the center of the vertical ellipse is the origin C(0,0), then h=0 and k=0, you can express the equation of the ellipse is:

`(x^2)/(b^2)+(y^2)/(a^2)=1`

The vertical axis is 20 units long, the center is the midpoint of the vertical axis, so the distance between the center and the vertices of the vertical ellipse is half the length of the major axis:

`\begin{gathered} a=\frac{\text{major}-\text{axis}}{2} \\ a=(20)/(2) \\ a=10 \end{gathered}`

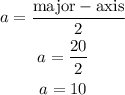
The horizontal axis is 12 units long, the center of the ellipse is the midpoint of the horizontal axis. The distance between the center and the co-vertices is half the length of the minor axis:

`\begin{gathered} b=\frac{\min or-\text{axis}}{2} \\ b=(12)/(2) \\ b=6 \end{gathered}`

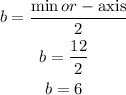
Replace both values on the equation:

`(x^2)/(6^2)+(y^2)/(10^2)=1`

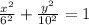
Solve the exponents and the equation of the vertical ellipse is:

`(x^2)/(36)+(y^2)/(100)=1`