Question

How many such cubes are required to completely pack the prism without any gap or overlap?2885761,1521,636

Answer 1

Given:

Cuboid:

`\begin{gathered} Length,l=4\text{ inches} \\ Breadth,b=(3)/(4)\text{ inch} \\ Height,h=1(2)/(4)inches \end{gathered}`

Cube:

`\text{Side, a}=(1)/(4)inch`

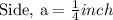
To find: The number of cubes required to pack the prism completely.

Step-by-step explanation:

The formula is,

`\begin{gathered} n=\frac{\text{Volume of cuboid}}{\text{Volume of cube}} \\ n=(l* b* h)/(a^3) \end{gathered}`

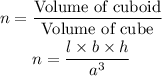
Substituting the given values in the above formula, we get,

`\begin{gathered} n=(4*(3)/(4)*1(2)/(4))/(((1)/(4))^3) \\ =(4*(3)/(4)*(6)/(4))/((1)/(64)) \\ =((9)/(2))/((1)/(64)) \\ =(9)/(2)*(64)/(1) \\ =9*32 \\ n=288 \end{gathered}`

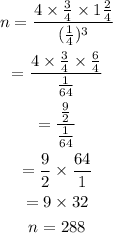
Thus, the number of cubs required to pack the prism is 288 cubes.

Final answer: 288 cubes