Step 1. First, let's find an expression to find how much money she can make.
We know that Carey has 23 saved, and can earn 8.75 per hour. In our expression "x" will represent the number of hours that she works:
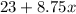
This expression represents the money she can make given that she already has 23, and makes 8.75 per hour "x" that she works.
Step 2. Define the inequality for the problem.
The items of clothing she wants to purchase cost 381.75, thus, the money she makes has to be equal to 381.75 or greater than that.
This is represented by the following inequality:
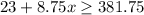
On the left side we have the expression for the money she can make, then the symbol greater than or equal to, and finally on the right side we have the amount she needs to have.
Step 3. Solve the inequality for x.
To solve for x, the first step is to subtract 23 to both sides of the inequality:
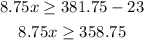
And then, divide both sides of the inequality by 8.75:
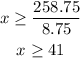
This tells us that Carey must work at least 41 hours to purchase the items of clothing.
Answer:

She has to work at least 41 hours.