Question

What is the probability that A occurs qiven that B occurs ?

Answer 1

Dependent events

A and B are dependent events. This means that the outcome of B affects the outcome of A.

We have that "the probability that A occurs given that B occurs" is symbolized by

P(A|B)

This is what we want to find.

We have that:

P(A): probability that event A occurs.

P(A) = 1/4

P(B): probability that event B occurs.

P(B) = 8/9

P(A&B): probability that both events A and B occurs.

P(A&B) = 1/5

We have that:

`\begin{gathered} P\mleft(A\&B\mright)=P\mleft(B\mright)\cdot P\mleft(A|B\mright) \\ \downarrow \\ (P(A\&B))/(P(B))=P(A|B) \end{gathered}`

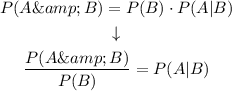
Replacing in the equation:

`\begin{gathered} (P(A\&B))/(P(B))=P(A|B) \\ \downarrow\text{ since }P\mleft(A\&B\mright)=(1)/(5)\text{ and }P\mleft(B\mright)=(8)/(9) \\ ((1)/(5))/((8)/(9))=P(A|B) \end{gathered}`

Since,

`((1)/(5))/((8)/(9))=(1)/(5)\cdot(9)/(8)=(9)/(40)`

Then

`P(A|B)=(9)/(40)`

Answer: 9/40