1 Answer

Ask a Question

Mehmetx · Answer 1 · 2023-10-09T15:10:50+0000

Given: The function below

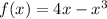
To Determine: the point of concave up

Solution

Factorize the function

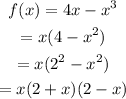
$\begin{gathered} f(x)=4x-x^3 \\ =x(4-x^2) \\ =x(2^2-x^2) \\ =x(2+x)(2-x) \end{gathered}$

The graph of the function is as shown below

It can be observed that the graph concave up at

$-\infty(B) To Determine: Where it concave down<p>From the graph, the function concave downward as shown below</p>[tex]\begin{gathered} concave\text{ downard:} \\ 0(C) To Determine the inflection point<p>From the graph, the inflection is the </p>[tex](0,0)$

Hence,

(A) f(x) concave up at (-∞, 0)

(B) concave down at (0, ∞)

(C) Inflection point at (0, 0)

f(x)=4x-x^3(A) Use interval notation to indicate where f(x) is concave up.Concave-example-1

0 Comments

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

0 Comments

Please log in or register to add a comment.

Other Questions