Given:
Interest rate = 10%
Money deposit = 2000
Find-:
Amount after
(1) One year
(2) Second year
(3) Three year
Explanation-:
The compound interest rate formula is:
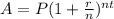
Where,

Foe one year
t=1
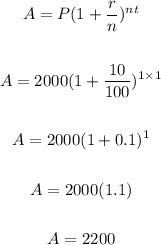
After one year amount is 2200.
(ii)
For 2 years
t = 2,
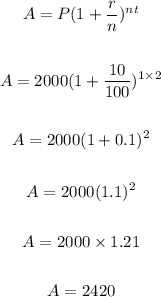
After two year amount is 2420.
(iii)
For three years
t=3
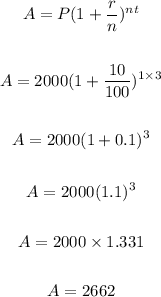
After 3 year amount is 2662