Question

Looking to receive help on practice question 103, thank you!

Answer 1

To convert the given polar equation to rectangular form, here are the steps.

1. Remember that sec θ = 1/cos θ. This means, the given polar equation can also be written as:

`r=(-3)/(\cos \theta)`

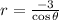
2. We can multiply cos θ to both sides of the function to remove the cos θ in the right side.

`\begin{gathered} r(\cos \theta)=(-3)/(\cos\theta)(\cos \theta) \\ r\cos \theta=-3 \end{gathered}`

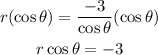
3. Since we know that x = r cos θ, we can say that x = -3. This is the rectangular form of the equation.

`x=-3`