Question

Hi can you help me with this question? And find out the answer.

Answer 1

Answer:
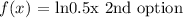
`f(x)\text{ = ln0.5x \lparen2nd option\rparen}`Step-by-step explanation:

Given:

The graph of a function

To find:

The function represented by the graph

To determine the right function, we will assign values to x in order to get the values of y. Then we will compare the y values with the y values on the graph

let x = 2, 5

`\begin{gathered} when\text{ x = 2} \\ a)\text{ }f(x)=\text{ e}*0.5x \\ f(x)\text{ = e}*0.5(2)\text{ = 2.718 \lparen wrong\rparen} \\ \\ b)\text{ }f(x)\text{ = ln0.5x} \\ f(x)\text{ = ln 0.5\lparen2\rparen = 0} \\ \\ c)\text{ }f(x)\text{ = e}^(0.5x) \\ f(x)\text{ = e}^(0.5(2))\text{ = 2.718 \lparen wrong\rparen} \\ \\ d)\text{ }f(x)\text{ = log0.5x} \\ f(x)\text{ = log0.5\lparen2\rparen = 0} \end{gathered}`

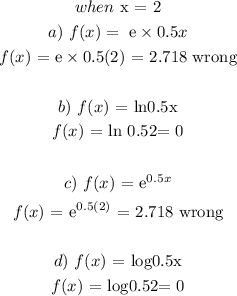
From the graph: when x = 2, y = 0

This means the likely functions are the 2nd and last option.

We will check for when x = 5 to ascertain the correct function:

`\begin{gathered} f(x)\text{ = ln0.5\lparen5\rparen} \\ f(x)\text{ = 0.916} \\ \\ f(x)\text{ = log0.5\lparen5\rparen} \\ f(x)\text{ = 0.398} \end{gathered}`

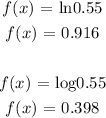
From the graph, the value of y is around 1 when x is 5

Since 0.916 is closer to 1, the function represented by the graph is f(x) ln0.5x