Question

COS X/1+sinx = sec x-tan x

Answer 1

Hello there. To solve this question, we'll have to remember some properties about trigonometric functions.

Given the expression:

`(\cos(x))/(1+\sin(x))`

We want to show that it is equal to

`\sec(x)-\tan(x)`

First, multiply the fraction by the following expression

`\begin{gathered} (1-\sin(x))/(1-\sin(x)) \\ \end{gathered}`

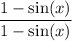
We choose this fraction for two reasons:

It does not change the expression, since we're multiplying it by 1

It will help in rewrite the expression in the denominator, using a product rule.

Okay. Multiplying the fractions, we get

`(\cos(x))/(1+\sin(x))\cdot(1-\sin(x))/(1-\sin(x))=(\cos(x)\cdot(1-\sin(x)))/((1+\sin(x))\cdot(1-\sin(x)))`

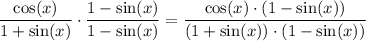
In the denominator, apply the rule of the product between the sum and difference:

`(a+b)(a-b)=a^2-b^2`

Hence we have

`(\cos(x)\cdot(1-\sin(x)))/(1-\sin^2(x))`

Using the fundamental trigonometric identity

`\cos^2(x)+\sin^2(x)=1`

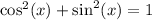
We write

`\cos^2(x)=1-\sin^2(x)`

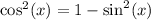
Therefore we get

`(\cos(x)\cdot(1-\sin(x)))/(\cos^2(x))`

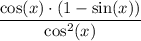
Simplify the fraction by a factor of cos(x)

`(1-\sin(x))/(\cos(x))`

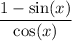
Break up the fraction as a sum of fractions

`(1)/(\cos(x))-(\sin(x))/(\cos(x))`

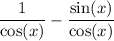
Knowing that

`\begin{gathered} \tan(x)=(\sin(x))/(\cos(x))\text{ and} \\ \\ \sec(x)=(1)/(\cos(x)) \end{gathered}`

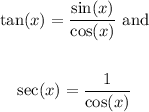
We get

`\sec(x)-\tan(x)`

Therefore we say that the equality holds and the statement is true.