Given the equation
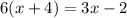
In other to solve the equation, the first step is to remove the bracket through expansion
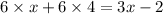
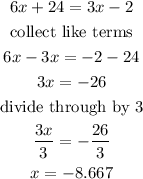
The likely error from the first step would be in the expansion
The first possible first step to solving the question is to expand 6(x+4)
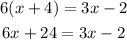
Solving through gives
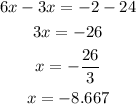
Hence, using the first method gives x=-8.667
The second possible first step to the equation is to divide both sides by multiplicative inverse of 6
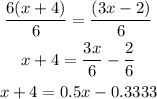
Solving through to get x will give

Hence, using the second method gives x=-8.667
from the two possible steps for solving the equation, the solution for x gives the same answer, x=-8.667
Hence, it does not matter which method used because we still arrived at the same answer