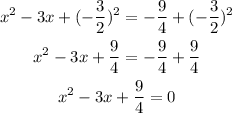Question

Rewrite the equation by completing the square4x^2-12x+9=0(x+__ )^2=__

Answer 1

We are asked to solve the below quadratic equation by completing the square;

`4x^2-12x+9=0`

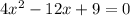
Step 1: We've got to rearrange the equation to have the constant term( the term without any variable) on the right hand side of the equation;

`4x^2_{}-12x=-9`

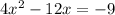
Step 2: We need the coefficient of x^2 to be 1, so we need to factor out 4 on the left hand side of the equation and divide both sides of the equation by 4;

`\begin{gathered} 4(x^2-3x)=-9 \\ x^2-3x=-(9)/(4) \end{gathered}`

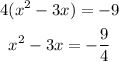
Step 3: To complete the square, we'll find 1/2 of the coefficient of x which is -3 and square it. Then we'll add to both sides of the equation;

`\begin{gathered} x^2-3x+(-(3)/(2))^2=-(9)/(4)+(-(3)/(2))^2 \\ x^2-3x+(9)/(4)=-(9)/(4)+(9)/(4) \\ x^2-3x+(9)/(4)=0 \end{gathered}`