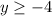1 Answer

Van Kichline · Answer 1 · 2024-01-02T08:46:53+0000

The given function is

$f(x)=\sqrt[]{x}$

then -f(x) is

$h(x)=-\sqrt[]{x}$

and f(x+2)-4 is

$g(x)=\sqrt[]{x+2}-4$

Now, lets make the graph of -f(x) and f(x+2)-4:

Graph A is in purple color and graph B is in black color. The original function is in green color.

The domain of the parent function f(x) is

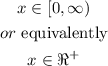
$\begin{gathered} x\in\lbrack0,\infty) \\ or\text{ equivalently} \\ x\in\mathfrak{\Re ^+} \end{gathered}$

and the range is

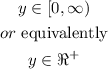
$\begin{gathered} y\in\lbrack0,\infty) \\ or\text{ equivalently} \\ y\in\mathfrak{\Re ^+} \end{gathered}$

For the purple curve, the domain is

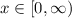
$x\in\lbrack0,\infty)$

and the range is

$y\le0$

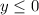
For the black curve, the domain is

$x\ge-2$

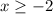
and the range is

$y\ge-4$

Please log in or register to add a comment.