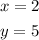Question

Solve the system by graphing.x+y=7-3x+y=-1

Answer 1

Step 1. In order to make it easier to graph the equations, we for y in each equation.

The equations we have are:

`\begin{gathered} x+y=7 \\ -3x+y=-1 \end{gathered}`

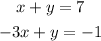
Solving for y in the first one (moving x as a -x to the right-hand side:

`y=-x+7`

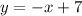
Solving for y in the second one (moving -3x as a +3x to the right-hand side):

`y=3x-1`

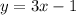
Step 2. Now the system of equations is:

`\begin{gathered} y=-x+7 \\ y=3x-1 \end{gathered}`

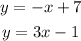
To graph the equations, we need the slope and y-intercept of the line that each equation represents.

To find them, we compare them with the general slope-intercept equation:

`y=mx+b`

where m is the slope and b is the y-intercept.

--> The slope represents how many units the line moves in the y-axis compared to a movement in the x-direction.

--> The y-intercept is the point where the line crosses the y-axis.

In our first equation:

`\begin{gathered} y=-x+7 \\ m=-1 \\ b=7 \end{gathered}`

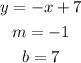
A y-intercept of 7 means that the line will cross the y-axis at 7, and a slope of -1 indicates that the line moves 1 down in the y-direction while it moves 1 in the x-direction.

This line is shown in red:

And for the second line:

`\begin{gathered} y=3x-1 \\ m=3 \\ b=-1 \end{gathered}`

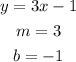
A y-intercept ''b'' of -1 indicates that the line will cross the y-axis at -1, and a slope of 3 indicates that the line will move 3 up in the y-direction dor every 1 unit in the x-direction, this is shown in green in the following diagram:

Step 3. Find the point where the two lines intersect and that will be the solution to the system of equations:

That point is:

`(2,5)`

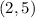
Where the x-value is 2 and the y-value is 5.

Answer:

`\begin{gathered} x=2 \\ y=5 \end{gathered}`