Question

Determine the number of solutions for the following system of linear equations. If there is only onesolution, find the solution.6x - 4y - 5z = 2- x - 3y + z = -27x - 6y – 4z = 4AnswerKeypadKeyboard ShortcutsSelecting an option will enable input for any required text boxes. If the selected option does not have anyassociated text boxes, then no further input is required.O No SolutionO Only One Solutionr =y =Z =O Infinitely Many Solutions

Answer 1

Before we solve the system, let's verify if it has a solution, let's do the determinant test:

`\det \begin{bmatrix}{6} & {-4} & {-5} \\ {-1} & {-3} & {6} \\ {7} & {-6} & {-4}\end{bmatrix}=1`

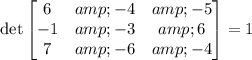
The determinant is 1, so it's different from zero, then the system has a unique solution.

Now let's determine the unique solution, I'll solve it using Cramer's Rule, because we already have the determinant of the coefficient matrix

Then

`\Delta=\mleft|\begin{matrix}6 & -4 & -5 \\ -1 & -3 & 6 \\ 7 & -6 & -4\end{matrix}\mright|=1`

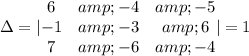
Now let's evaluate the determinants with the coefficients

`\Delta_x=\mleft|\begin{matrix}2 & -4 & -5 \\ -2 & -3 & 6 \\ 4 & -6 & -4\end{matrix}\mright|=-88`

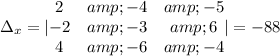
Now the variable y

`\Delta_y=\mleft|\begin{matrix}6 & 2 & -5 \\ -1 & -2 & 6 \\ 7 & 4 & -4\end{matrix}\mright|=-70`

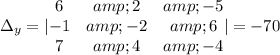
And the last one

`\Delta_z=\mleft|\begin{matrix}6 & -4 & 2 \\ -1 & -3 & -2 \\ 7 & -6 & 4\end{matrix}\mright|=-50`

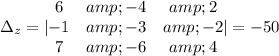
The solution will be

`\begin{gathered} x=(\Delta_x)/(\Delta)=(-88)/(1)=-88 \\ \\ y=(\Delta_y)/(\Delta)=(-70)/(1)=-70 \\ \\ z=(\Delta_z)/(\Delta)=(-50)/(1)=-50 \end{gathered}`

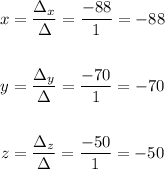
Final answer:

Only one solution

x = -88

y = -70

z = -50