We have to use the trigonometric ratios to find the lengths of the missing sides.
We know the measure of the angle O and the length of its opposite side DT.
We can find the value of the hypotenuse OT with the ratio:
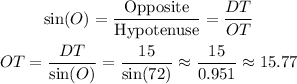
We can find the length of the adyacent side OD with the ratio:
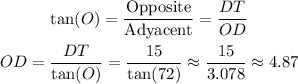
To complete the missing angles, we take into account that one of the angles, D, is a right angle, so its measure is 90°.
Angle T and angle O are complementary, so they add 90° between the two.
Then, angle T will have a measure of 90-72 = 18°.
Answer:
Sides:
OD = 4.87
OT = 15.77
Angles:
m∠O = 90°
m∠T = 18°