Given
A positive integer is 48 more than 23 times another.
Their product is 12188.
To find the two integers.
Step-by-step explanation:
Let x and y be the two positive integers.
Since a positive integer is 48 more than 23 times another.
Then,

Also, since their product is 12188.
Then,
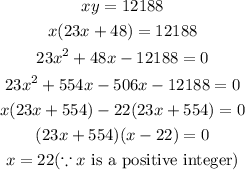
That implies,
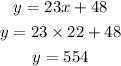
Hence, the two integers are 22 and 554 respectively.