Question

In Duluth, about 45% of dogs like the snow. If you ask the owners of 200 dogs, what is the (approximate) probability that fewer than 100 of the dogs like snow?I want answer and explanation.

Answer 1

Step-by-step explanation

We need to use the Normal Approximation to the Binomial Distribution with the probability and the mean:

p= 0.45

n=200

P(X < 100) = P(X <= 99)

Mean = np = 200(0.45) = 90

Standard Deviation = √(npq) = √(200*0.45*0.55) = √(49.5) = 7.03

Now, we need to compute the value of z-score:

`z=(99-90)/(7.03)=(9)/(7.03)=1.28`

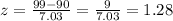
Now, computing the probability in a z-table:

`P(z<1.28)=0.8997`

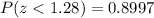
In conclusion, the probability is 0.8997