Given
geometric sequence
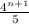
Find
Common ratio and first four terms of sequence
Step-by-step explanation
as we have given nth term =
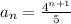
now put values of n to find the first four terms
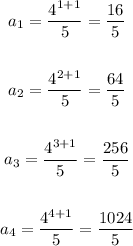
common ratio = second term divided by first term
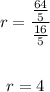
Final Answer
Common ratio = 4
sequence = 16/5 , 64/5 , 256/5 and 1024/5