Question

How much would you need to deposit in an account now in order to have $4000 in the account in 5 years?Assume the account earns 7% interest compounded monthly.

Answer 1

$2821.67.

Explanation:

The formula for calculating the amount, A in an account for an initial deposit, P compounded k times in a year for t years at a rate of r% is:

`A=P(1+(r)/(k))^(kt)`

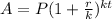
In the given problem:

• The amount that will be in the account, A(t) = $4,000

,

• Time, t=5 years

,

• Rate, r = 7% = 0.07

,

• k=12 (compounded monthly)

We want to find the value of P.

`\begin{gathered} 4000=P(1+(0.07)/(12))^(12*5) \\ \implies P=4000/(1+(0.07)/(12))^(12*5)=4000/1.4176 \\ P=\$2821.67 \end{gathered}`

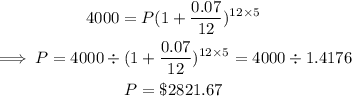
You would need to deposit $2821.67.

Q