Given:
Speed of light = 3 x 10⁸ m/s
Let's solve for the following:
• (a). How many miles does a pulse of light travel in a time interval of 0.1 s, which is about the blink of an eye?
Apply the formula:
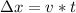
Where:
v is the speed of light
t is the time.
Thus, we have:
![\begin{gathered} \Delta x=3.0*10^8*0.1 \\ \\ \Delta x=3.0\operatorname{*}10^7\text{ m} \end{gathered}]()
Now let's convert the answer from meters to miles.
Where:
1 mile = 1609.34 meters
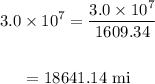
Δx = 18641.14 mi
• (b). Compare this distance to the diameter of Earth.
Apply the formula:

Where:
r = 6.38 x 10⁶ m.
Thus, we have:
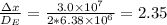
ANSWER:
• (a). 18641.14 mi
,
• (b). 2.35