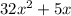Given:
Area of large rectangle = (8x + 1)(5x)
Area of small rectangle = (4x)(2x)
To find area of the shaded region, subtract the area of the small rectangle from the large rectangle.
We have:
Area of large rectangle =
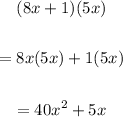
Area of small rectangle =
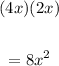
Area of shaded region =
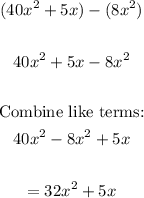
Therefore, the area of the shaded region is = 32x² + 5x
ANSWER: