Question

A pilot wishes to fly 2500km due South. The air speed of the plane is 300km/h and there is a wind of 50km/h from the West. What heading should the pilot take and what is the time required to complete the flight?

Answer 1

Since there is a wind speed of 50 km/h to the west, this speed needs to be compensated by the heading of the plane.

If we decompose the plane speed, one component will be used to cancel out the wind speed:

To find the orientation theta, we can calculate the east component of the plane speed and equate it to the wind speed:

`\begin{gathered} V_{\text{east}}=V_{\text{wind}} \\ V\cdot\sin (\theta)=50 \\ 300\cdot\sin (\theta)=50 \\ \sin (\theta)=(50)/(300)=(1)/(6) \\ \theta=\sin ^(-1)((1)/(6)) \\ \theta=9.59\degree \end{gathered}`

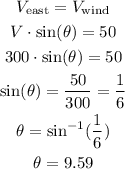
Now, let's calculate the south component:

`\begin{gathered} V_{\text{south}}=V\cdot\cos (9.59\degree) \\ V_{\text{south}}=300\cdot0.986 \\ V_{\text{south}}=295.8\text{ km/h} \end{gathered}`

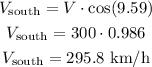
Calculating the required time of flight, we have:

`\begin{gathered} \text{distance}=\text{speed}\cdot\text{time} \\ 2500=295.8\cdot t \\ t=(2500)/(295.8) \\ t=8.45\text{ hours} \end{gathered}`

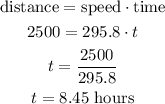
Therefore the orientation is 9.59° east of south and the time required is 8.45 hours.