Question : the function in the question is given below as
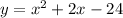
Step 1: Calculate the x-intercept
The x-intercept for any curve is the value of the x coordinate of the point where the graph cuts the x-axis, or we can say that the x-intercept is the value of the x coordinate of a point where the value of the y coordinate is equal to zero.
Equating the equation above to zero (0)
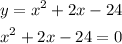
Solving using the quadratic formula below,
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/rxvf73usjbbwyik14knxdemoz21vfz2ufc.png)
The general formula of a quadratic equation is given below

By comparing the coefficient, we will have the values to be
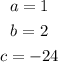
Step 2: Substitute the values into the quadratic formula to get the values of x
![\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ x=\frac{-2\pm\sqrt[]{2^2-(4*1*-24)}}{2*1} \\ x=\frac{-2\pm\sqrt[]{4^{}+96}}{2} \\ x=\frac{-2\pm\sqrt[]{100}}{2} \\ x=(-2\pm10)/(2) \\ x=(-2+10)/(2)\text{ or }x=(-2-10)/(2) \\ x=(8)/(2)\text{ or x=}\frac{\text{-12}}{2} \\ x=4\text{ or x=-6} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/8q2km7ib8kg60b5vbamc210rg24bag99h6.png)
Hence,
The x-intercepts are
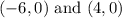
x-intercepts are (-6,0) and (4,0)
Step 3: Calculate the coordinate of the y-intercept
The point where a line or curve crosses the y-axis of a graph.
In other words: find the value when x equals 0
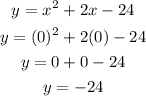
Hence,
The y-intercept is
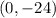
The y-intercept is (0,-24)
Below is the graph of the function on the question with its x-intercepts and y-intercepts
Step 4: Determine if the graph is minimum or maximum
The first step is to determine whether your equation gives a maximum or minimum. This can be done by looking at the x^2 term. If this term is positive, the vertex point will be a minimum; if it is negative, the vertex will be a maximum.
The coefficient of the x^2 term is a positive 1
Hence,
The equation
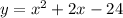
is a minimum quadratic graph