Question

The scores of 12th-grade students on the National Assessment of Educational Progress year 2000 mathematics test have a distribution that is approximately Normal with mean μ = 300 and standard deviation σ = 35. (a) Choose one 12th-grader at random. What is the probability that his or her score is higher than 300? Higher than 335? Explain and show your work. (b) Now choose an SRS of four 12th-graders and calculate their mean score x. If you did this many times, what would be the mean and standard deviation of all the x-values? Explain and show your work. (c) What is the probability that the mean score for your SRS is higher than 300? Higher than 335? Explain and show your work.

Answer 1

a) To find the probability that the score is higher than 300 you have to find the Z-score for 300, by using the formula:

`\begin{gathered} Z=(x-\mu)/(\sigma) \\ Z=(300-300)/(35)=(0)/(35)=0 \end{gathered}`

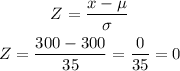
The probability of x>300 P(z>0)=1-P(z<=0)

Using the Standard Normal Cumulative Probability Table, P(z<=0)=0.5

Then,

`P(Z>0)=1-0.5=0.5`

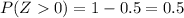
Now, you can do the same to find the probability that the score is higher than 335, let' see:

`Z=(335-300)/(35)=(35)/(35)=1`

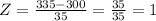
The probability of x>335 is P(Z>1), then

`P(Z>1)=1-P(Z\leq1)=1-0.8413=0.1587`

These results mean that it is a 50% of probability that the score of the student chosen is greater than 300, and a 15.87% of probability that the score is greater than 335.

b) SRS=4, their mean score will be the same as the mean of the population = 300, the standard deviation of the sample is the standard deviation of the population divided by √n (n is the size of the sample=4).

`\mu=300\text{ and }\sigma=\frac{35}{\sqrt[]{4}}=17.5`

c) The probability that the mean score for the SRS is higher than 300 is:

`\begin{gathered} Z=(x-\mu)/(\sigma) \\ Z=(300-300)/(17.5)=(0)/(17.5)=0 \end{gathered}`
`P(Z>0)=1-P(Z\leq0)=1-0.5=0.5`

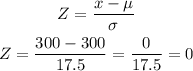
The probability that the mean score for the SRS is higher than 335 is:

`Z=(335-300)/(17.5)=2`
`P(Z>2)=1-P(Z\leq2)=1-0.9772=0.0228`

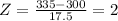
These results mean that it is a 50% of probability that the mean score of the SRS is greater than 300, and a 2.28% of probability that the mean score is greater than 335.