Question

The equation of Line 1 is y=-2x + 7. Line 2 passesthrough the points (2, 3) and (4, 4). Which statementis true about Line 1 and Line 2?Line 1 and Line 2 are perpendicularO Line 1 is longer than Line 2Line 1 has the same y-intercept as Line 2Line 1 and Line 2 are parallel

Answer 1

Line 1 is given as

`y=-2x+7`

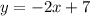
let's find the equation of line 2, it passes through points (2, 3) and (4, 4)

The slope is

`\begin{gathered} m=(4-3)/(4-2) \\ m=(1)/(2) \end{gathered}`

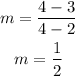
The slope of line 2 is 1/2

If the two lines are perpendicular, then the product of their slope will be = -1, that is

`\begin{gathered} m_1m_2=-1 \\ slope\text{ of line 1 m}_1=-2 \\ slope\text{ of line 2, m}_2=(1)/(2) \\ -2*(1)/(2)=(-2)/(2)=-1 \\ \end{gathered}`

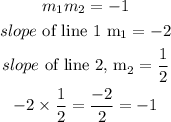
Since the product of their slope = -1

Hence Line 1 and Line 2 are perpendicular