Answer: 74.43%
Let us first list down the probabilities of the machine working.
First is the probability that none of the components will fail. We can write this probability as:
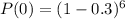
Next, the probability that one of the components will fail. This will give us:
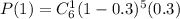
Then, the probability that 2 of the components will fail.
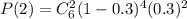
Adding all of these probabilities and we will have:
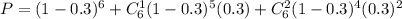
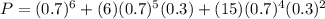
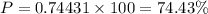
Therefore, the probability that the machine will be working would be 74.43%.