Solution
For this case we have the following random variable:
X= amount spend on average for groceries by one person
And we have the following properties:
mean= 52
sd= 14
The distribution of the variable is normal
We can find the middle 50% using a graph like this one:
We can find two quantiles from the normal distribution that accumulates 25% of the area on each tail of the distribution and we have:
Z= -0.674 and 0.674
Now we can use the z score formula given by:
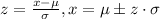
So then we have:
Minimum= 52 - 0.674*14 = 42.56
Minimum= 52 + 0.674*14 = 61.44