Question

Hello, I need some assistance with this homework question, please? This is for my precalculus homework. Q11

Answer 1

Step-by-step explanation

The vertical asymptote

for the given function

`T(x)=(x^3)/(x^4-81)`

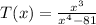
According to the formula

The denominator will be undefined when

`\begin{gathered} x^4-81=0 \\ x=\sqrt[4]{81} \\ x=3,\text{ x=-3} \\ x= \end{gathered}`

The vertical asymptotes are

`x=-3,3`

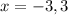
For the horizontal function

`\mathrm{If\:denominator's\:degree\:>\:numerator's\:degree,\:the\:horizontal\:asymptote\:is\:the\:x-axis:}\:y=0.`

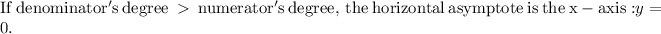
Since the denominator degree is higher than the numerator

Then

The horizontal asymptote is

`y=0`

For the oblique asymptote

Since the degree of the numerator is not one degree greater than the denominator, then there are no slant asymptotes.

There are no oblique asymptote