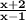One way of simplifying the given expression is by factoring them, and then simplifying the common terms.
So, we need to write:
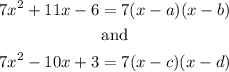
The constants a and b are the zeros of the first expression, and the constants c and d are the zeros of the second expression.
So, we can find those zeros using the quadratic formula. We obtain, for the first expression:
![\begin{gathered} x=\frac{-11\pm\sqrt[]{11^(2)-4(7)(-6)}}{2(7)} \\ \\ x=\frac{-11\pm\sqrt[]{289}}{14} \\ \\ x=(-11\pm17)/(14) \\ \\ a=(-11-17)/(14)=-2 \\ \\ b=(-11+17)/(14)=(6)/(14)=(3)/(7) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/u0j8axyulaeaffie3j6sh132gitkxjvtx1.png)
And, for the second expression, we obtain:
![\begin{gathered} x=\frac{-(-10)\pm\sqrt[]{(-10)^(2)-4(7)(3)}}{2(7)} \\ \\ x=\frac{10\pm\sqrt[]{16}}{14} \\ \\ x=(10\pm4)/(14) \\ \\ c=(10-4)/(14)=(6)/(14)=(3)/(7) \\ \\ d=(10+4)/(14)=1 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/4bgrslz4ejslo2f7ieeitn93j1zswx17ga.png)
Then, we can write:

Thus, the given function can be simplified as follows:

Therefore, the answer is: