Question

A fisherman in a stream 30 cm deep looks downward into the water and sees a rock on the stream bed. How deep does the stream appear to the fisherman? Let the index of refraction of the water equal 1.33O 26cmO 40cmO 34cmO 23cm

Answer 1

Given:

The depth of the stream, d=30 cm

The refractive index of water, n=1.33

To find:

The apparent depth of the stream.

Step-by-step explanation:

Let the eye of the fisherman is at a large height from the surface of the water.

Thus,

`\sin(i)=(x)/(d)`

Where i is the angle of incidence and r is the opposite side of the angle of incidence.

And,

`\sin(r)=(x)/(h)`

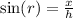
Where r is the angle of refraction and h is the apparent depth of the stream.

The refractive index of the air is n_a=1.

From snell's law,

`n_a\sin r=n\sin i`

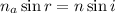
On substituting the known values,

`\begin{gathered} 1*(x)/(h)=1.33*(x)/(d) \\ \implies h=(d)/(1.33) \\ =(30)/(1.33) \\ =23\text{ cn} \end{gathered}`

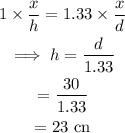
Final answer:

The correct answer is option d.