Question

Starting from rest, a car accelerates at 2.0 m/s2 up a hill that is inclined 5.5° above the horizontal. How far (a) horizontally and (b) vertically has the car traveled in 12 s?

Answer 1

Given data:

* The acceleration of the car is,

`a=2ms^(-2)^{}`

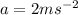
* The angle of the inclined plane is 5.5 degree.

* The time taken by the car is 12 s.

* The initial velocity of the car is 0 m/s.

Solution:

By the kinematics equation, the final velocity of the car on the inclined plane is,

`v-u=at`

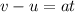
where v is the final velocity, u is the initial velocity, a is the acceleration, and t is the tiem taken,

Subsituting the known values,

`\begin{gathered} v-0=2*12 \\ v=24\text{ m/s} \end{gathered}`

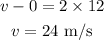
By the kinematics equation, the distance tarveled by the car on the inclined plane is,

`v^2-u^2=2aS`

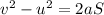
where S is the distance tarveled on the inclined plane,

Substituting the known values,

`\begin{gathered} 24^2-0=2*2* S \\ 576=4* S \\ S=(576)/(4) \\ S=144\text{ m} \end{gathered}`

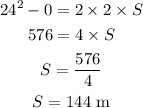
The diagrammatic representation of the car on the inclined plane is,

The distance traveled by the car in the horizontal direction or along x-axis is,

`\begin{gathered} S_x=S\cos (5.5^(\circ)) \\ S_x=144*\cos (5.5^(\circ)) \\ S_x=143.34\text{ m} \end{gathered}`

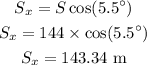
Thus, the distance tarveled by the car in the horizontal direction is 143.34 meter.

The distance tarveled by the car in the vertical direction or y-axis is,

`\begin{gathered} S_y=S\sin (5.5^(\circ)) \\ S_y=144*\sin (5.5^(\circ)) \\ S_y=13.8\text{ m} \end{gathered}`

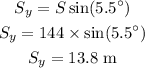
Thus, the distance tarveled by the car in the vertical direction is 13.8 meter.