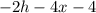Question

O GRAPHS AND FUNCTIONSFinding a difference quotient for a linear or quadratic function

Answer 1

Given the question in the image, the following are the solution steps to answer the question.

STEP 1: Write the given difference quotient formula

`(f(x+h)-f(x))/(h)`

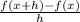
STEP 2: Write the given function f(x)

`f(x)=-2x^2-4x+7`

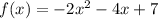
STEP 3: Get f(x+h)

`\begin{gathered} f(x)=-2x^2-4x+7,\text{ we n}eed\text{ to get }f(x+h) \\ f(x+h)=-2(x+h)^2-4(x+h)+7 \\ -2(x+h)^2-4(x+h)+7=-2(x^2+2xh+h^2)-4x-4h+7 \\ \Rightarrow-2x^2-4xh-2h^2-4x-4h+7 \\ \Rightarrow-2x^2-2h^2-4xh-4x-4h+7 \end{gathered}`

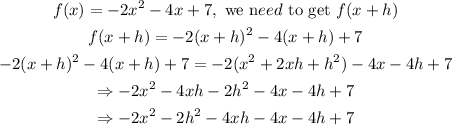
STEP 4: Rewrite the expression by substitution

`\begin{gathered} (f(x+h)-f(x))/(h)\Rightarrow(-2x^2-2h^2-4xh-4x-4h+7-(-2x^2-4x+7))/(h) \\ \Rightarrow\frac{-2x^2-2h^2-4xh-4x-4h+7+2x^2+4x-7_{}}{h} \\ Re-\text{arrange the expression} \\ (-2x^2+2x^2-2h^2-4xh-4x+4x-4h+7-7)/(h) \\ \Rightarrow(-2h^2-4xh-4h)/(h) \\ \Rightarrow(-h(2h))/(h)-((4x)h)/(h)-(h(4))/(h) \\ \Rightarrow-2h-4x-4 \end{gathered}`

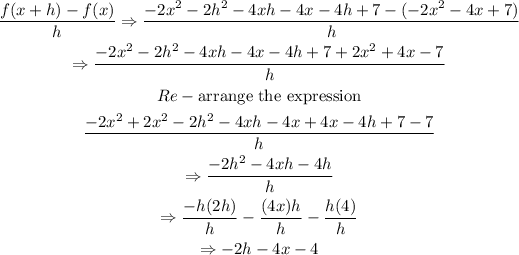
Hence, the result of the simplification is:

`-2h-4x-4`